Skip to main content

​
From Single Blocks to Entire Chains

We’ve seen how PoEM measures the exact work in a single block. But how do we compare entire blockchains? This is where total entropy comes in. Think of it like this:
  • Single block: “How hard was this math problem?”
  • Entire blockchain: “How hard was this entire series of math problems?”

​
Why Entropy Instead of “Work”?

Entropy is a physics concept that measures randomness or disorder. When miners find a block, they’re essentially reducing randomness by finding a very specific, ordered hash. The Key Insight: The amount of randomness removed (entropy reduced) directly corresponds to the energy spent creating that order. Real-world analogy:
  • Messy room (high entropy) → Clean room (low entropy)
  • Energy required to organize = Entropy reduced
  • More organized = More energy spent = Lower entropy

​
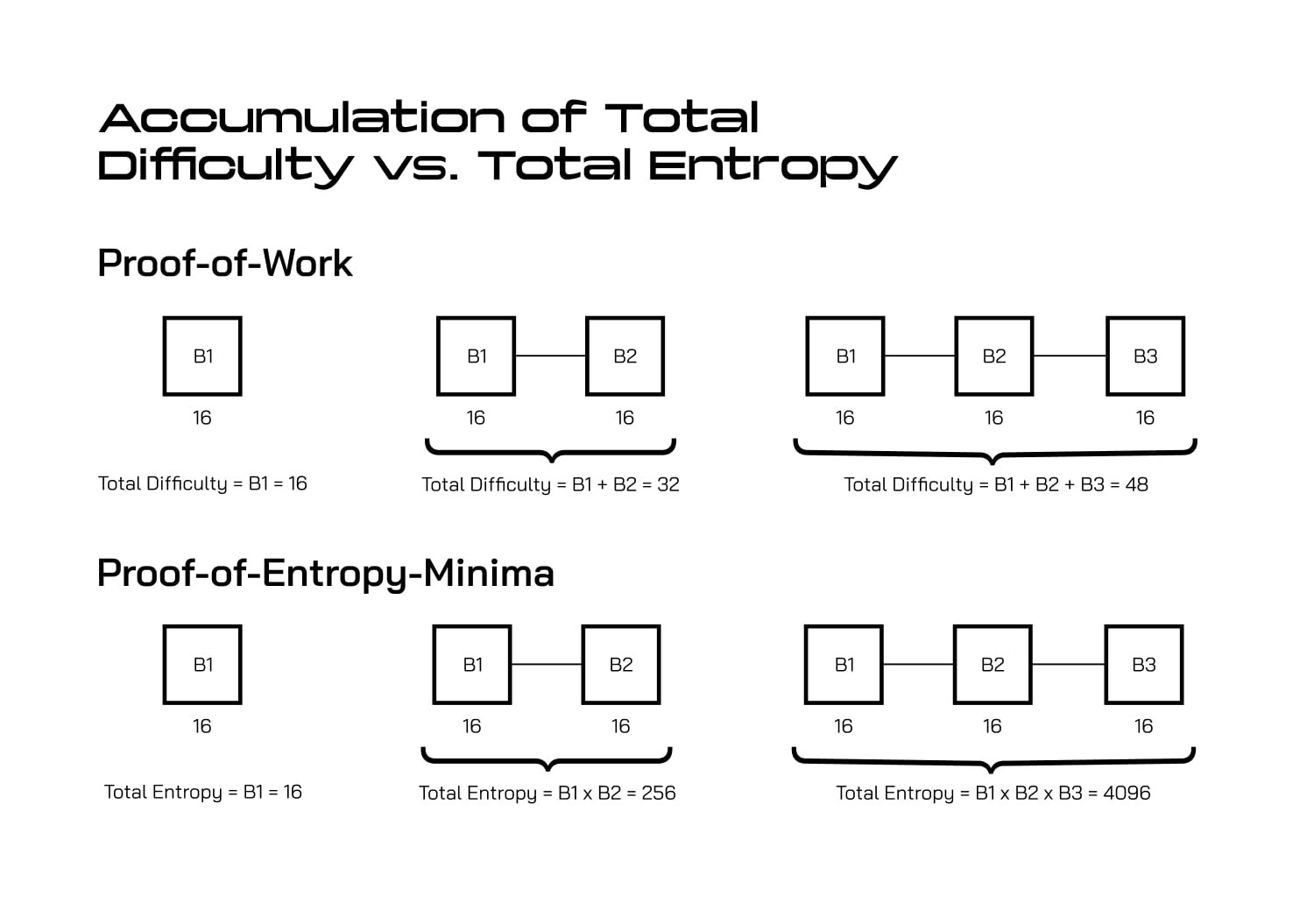
Geometric vs Linear: Why It Matters

Traditional PoW (Linear Addition):
  • Block 1: 16 difficulty points
  • Block 2: 16 difficulty points
  • Block 3: 16 difficulty points
  • Total: 16 + 16 + 16 = 48 points
PoEM (Geometric Multiplication):
  • Block 1: Removes 1/65536 of possible states
  • Block 2: Removes 1/65536 of remaining states
  • Block 3: Removes 1/65536 of remaining states
  • Total: (1/65536) × (1/65536) × (1/65536) = Much more security
Why Multiplication is Better:
  • Exponential security: Each block makes the chain exponentially harder to recreate
  • Real probability: Reflects the actual odds of recreating the work
  • Better comparison: More accurately measures which chain required more total energy
Think of it like compound interest: adding 10% three times gives you 130%, but compounding 10% three times gives you 133.1%. The difference becomes massive over many blocks.

​
Step-by-Step Calculation

​
Step 1: Calculate Single Block Entropy

For each block, we calculate how much randomness it removed: Simple Version: More leading zeros = more randomness removed Precise Formula: 
Block Entropy = 1 / (2^leading_zeros)
Example:
  • Block with 16 leading zeros: 1/65,536 states removed
  • Block with 17 leading zeros: 1/131,072 states removed (twice as rare!)

​
Step 2: Calculate Chain Total

For an entire blockchain, we multiply all the individual block entropies together: Formula: 
Total Chain Entropy = Block1 × Block2 × Block3 × ...
Example 3-Block Chain:
  • Block 1: 1/65,536
  • Block 2: 1/65,536
  • Block 3: 1/131,072
  • Total: (1/65,536) × (1/65,536) × (1/131,072) = 1 in 563 trillion
This means recreating this 3-block chain would require, on average, 563 trillion attempts!

​
Practical Implementation: Using Logarithms

The Problem: Those numbers get huge fast! After just 10 blocks, we’d be dealing with numbers so large they’re impossible to store efficiently. The Solution: Instead of storing the actual multiplication results, we use logarithms to convert multiplication into addition. How It Works:
  • Traditional storage: 1/65,536 × 1/65,536 × 1/131,072 = 0.000000000000234
  • Logarithmic storage: 16 + 16 + 17 = 49 bits of entropy
Benefits:
  • Manageable numbers: Addition instead of astronomical multiplication
  • Exact precision: No loss of accuracy in comparisons
  • Efficient storage: Quai uses 64 bits to store total entropy per chain
  • Easy comparison: Higher entropy number = more secure chain
The Final Formula: 
Total Chain Entropy (in bits) = Block1_bits + Block2_bits + Block3_bits + ...
This mathematical trick allows Quai to precisely compare chains of any length while keeping the computation practical for real-world use.
Key Takeaway: PoEM measures the exact probability of recreating any blockchain, giving it perfect objectivity when choosing between competing chains. The chain that would be hardest to recreate always wins.
⌘I