​
단일 블록에서 전체 체인으로

PoEM이 단일 블록에서 정확한 작업을 측정하는 방법을 살펴봤습니다. 하지만 전체 블록체인을 어떻게 비교할까요? 여기서 총 엔트로피가 등장합니다. 다음과 같이 생각해보세요:
  • 단일 블록: “이 수학 문제가 얼마나 어려웠는가?”
  • 전체 블록체인: “이 전체 일련의 수학 문제가 얼마나 어려웠는가?”

​
왜 “작업” 대신 엔트로피인가?

엔트로피는 무작위성이나 무질서를 측정하는 물리학 개념입니다. 채굴자가 블록을 찾을 때, 그들은 본질적으로 매우 특정하고 질서 있는 해시를 찾아 무작위성을 줄이고 있습니다. 핵심 통찰: 제거된 무작위성의 양(엔트로피 감소)은 그 질서를 만들기 위해 소비된 에너지와 직접적으로 일치합니다. 실제 비유:
  • 지저분한 방(높은 엔트로피) → 깨끗한 방(낮은 엔트로피)
  • 정리하는 데 필요한 에너지 = 엔트로피 감소
  • 더 정리될수록 = 더 많은 에너지 소비 = 더 낮은 엔트로피

​
기하급수적 대 선형: 왜 중요한가

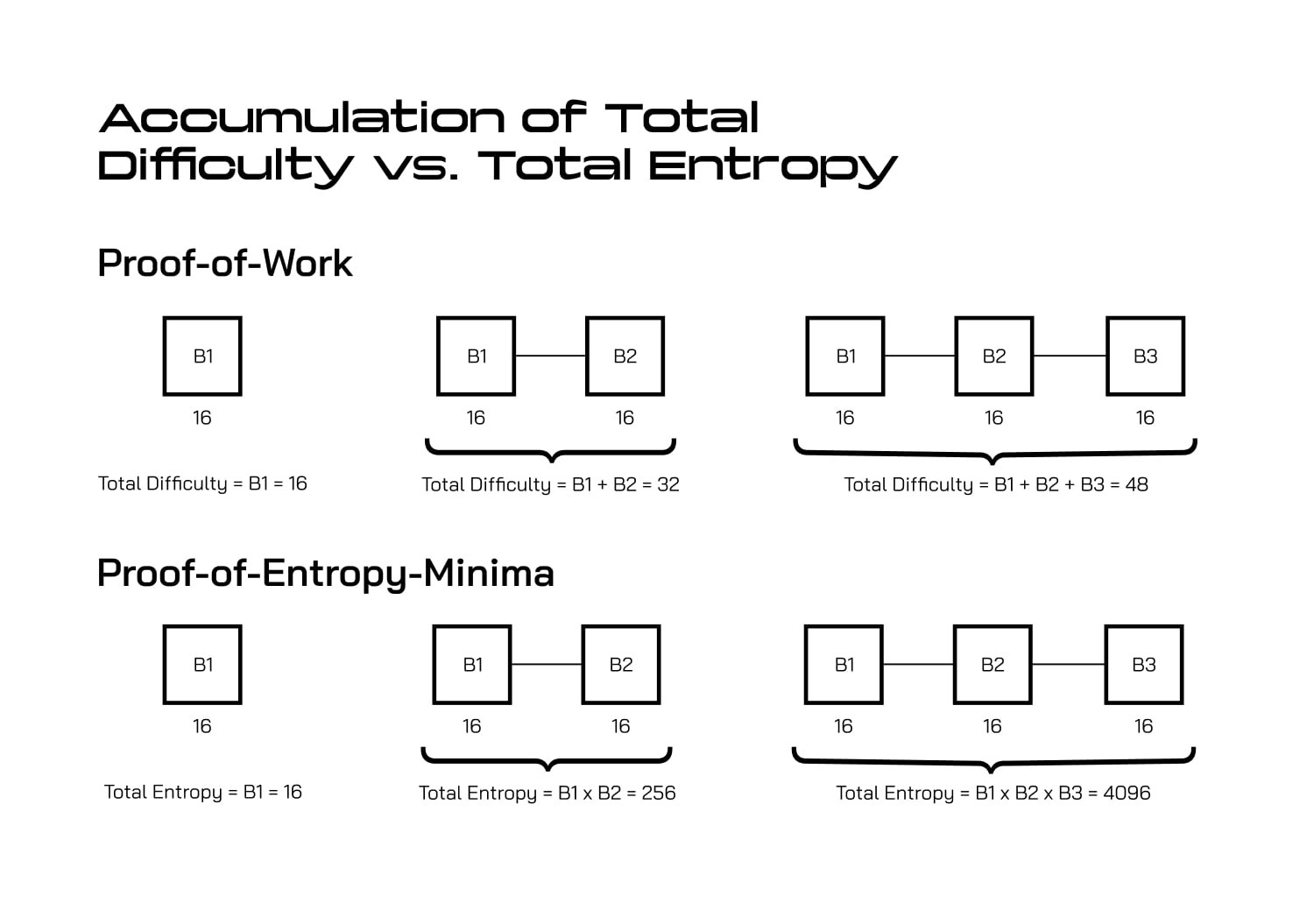
전통적인 PoW (선형 덧셈):
  • 블록 1: 16 난이도 포인트
  • 블록 2: 16 난이도 포인트
  • 블록 3: 16 난이도 포인트
  • 총합: 16 + 16 + 16 = 48 포인트
PoEM (기하급수적 곱셈):
  • 블록 1: 가능한 상태의 1/65536을 제거
  • 블록 2: 남은 상태의 1/65536을 제거
  • 블록 3: 남은 상태의 1/65536을 제거
  • 총합: (1/65536) × (1/65536) × (1/65536) = 훨씬 더 많은 보안
곱셈이 더 나은 이유:
  • 지수적 보안: 각 블록이 체인을 재생성하기 지수적으로 더 어렵게 만듭니다
  • 실제 확률: 작업을 재생성할 실제 확률을 반영합니다
  • 더 나은 비교: 어떤 체인이 더 많은 총 에너지를 필요로 했는지 더 정확하게 측정합니다
복리 이자처럼 생각해보세요: 10%를 세 번 더하면 130%가 되지만, 10%를 세 번 복리하면 133.1%가 됩니다. 많은 블록에 걸쳐 차이는 엄청나집니다.

​
단계별 계산

​
1단계: 단일 블록 엔트로피 계산

각 블록에 대해 제거한 무작위성의 양을 계산합니다: 간단한 버전: 더 많은 선행 0 = 더 많은 무작위성 제거 정확한 공식: 
블록 엔트로피 = 1 / (2^선행_영의_개수)
예시:
  • 16개의 선행 0을 가진 블록: 1/65,536개 상태 제거
  • 17개의 선행 0을 가진 블록: 1/131,072개 상태 제거 (두 배 희귀!)

​
2단계: 체인 총합 계산

전체 블록체인에 대해 모든 개별 블록 엔트로피를 함께 곱합니다: 공식: 
총 체인 엔트로피 = 블록1 × 블록2 × 블록3 × ...
3-블록 체인 예시:
  • 블록 1: 1/65,536
  • 블록 2: 1/65,536
  • 블록 3: 1/131,072
  • 총합: (1/65,536) × (1/65,536) × (1/131,072) = 563조 분의 1
이는 이 3-블록 체인을 재생성하려면 평균적으로 563조 번의 시도가 필요하다는 것을 의미합니다!

​
실용적 구현: 로그 사용

문제: 그 숫자들이 빠르게 거대해집니다! 단지 10개 블록 후에도 효율적으로 저장하기 불가능할 정도로 큰 숫자를 다루게 됩니다. 해결책: 실제 곱셈 결과를 저장하는 대신, 로그를 사용하여 곱셈을 덧셈으로 변환합니다. 작동 방식:
  • 전통적 저장: 1/65,536 × 1/65,536 × 1/131,072 = 0.000000000000234
  • 로그 저장: 16 + 16 + 17 = 49비트의 엔트로피
장점:
  • 관리 가능한 숫자: 천문학적 곱셈 대신 덧셈
  • 정확한 정밀도: 비교에서 정확도 손실 없음
  • 효율적 저장: Quai는 체인당 총 엔트로피를 저장하기 위해 64비트를 사용합니다
  • 쉬운 비교: 더 높은 엔트로피 숫자 = 더 안전한 체인
최종 공식: 
총 체인 엔트로피 (비트 단위) = 블록1_비트 + 블록2_비트 + 블록3_비트 + ...
이 수학적 기법을 통해 Quai는 임의 길이의 체인을 정확하게 비교하면서 계산을 실제 사용에 실용적으로 유지할 수 있습니다.
핵심 요점: PoEM은 모든 블록체인을 재생성할 정확한 확률을 측정하여 경쟁하는 체인 간 선택에서 완벽한 객관성을 제공합니다. 재생성하기 가장 어려운 체인이 항상 승리합니다.