从单个区块到整条链
我们已经看到 PoEM 如何测量单个区块中的确切工作量。但我们如何比较整条区块链?这就是总熵的作用。 这样想:- 单个区块:“这道数学题有多难?”
- 整条区块链:“这整个系列的数学题有多难?“
为什么是熵而不是”工作量”?
熵是一个物理概念,用来测量随机性或无序性。当矿工找到一个区块时,他们本质上是通过找到一个非常特定、有序的哈希来减少随机性。 关键洞察:移除的随机性量(减少的熵)直接对应于创造该秩序所花费的能量。 现实世界类比:- 混乱的房间(高熵)→ 整洁的房间(低熵)
- 组织所需的能量 = 减少的熵
- 更有序 = 花费更多能量 = 更低熵
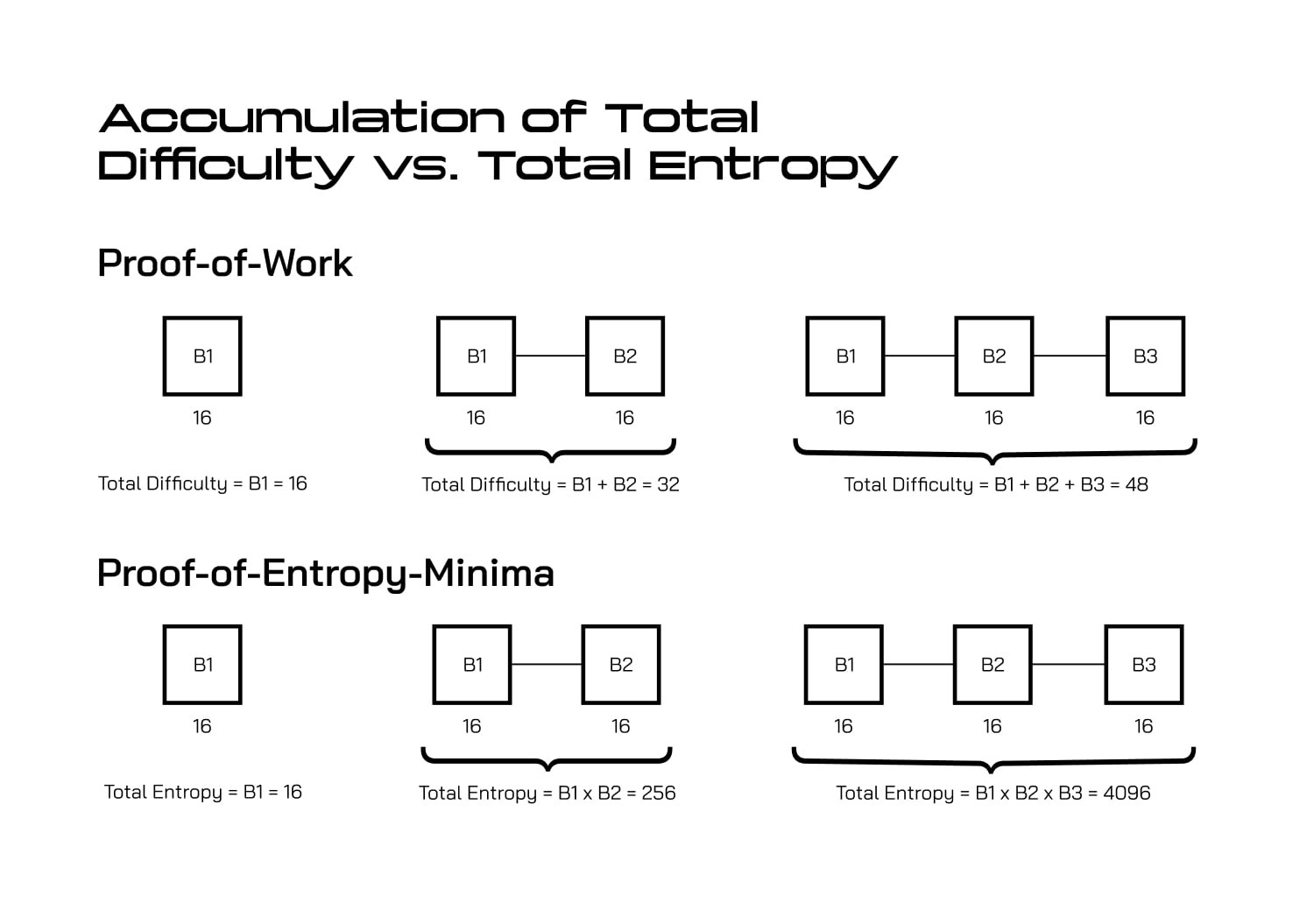
几何 vs 线性:为什么重要
传统 PoW(线性相加):- 区块 1:16 难度点
- 区块 2:16 难度点
- 区块 3:16 难度点
- 总计:16 + 16 + 16 = 48 点
- 区块 1:移除 1/65536 的可能状态
- 区块 2:移除剩余状态的 1/65536
- 区块 3:移除剩余状态的 1/65536
- 总计:(1/65536) × (1/65536) × (1/65536) = 更高的安全性
- 指数安全性:每个区块使链的重建变得指数级困难
- 真实概率:反映重建工作的实际几率
- 更好比较:更准确地测量哪条链需要更多总能量
想象成复利:3次加10%给你130%,但3次复合10%给你133.1%。在许多区块上,差异会变得巨大。
逐步计算
步骤 1:计算单个区块熵
对于每个区块,我们计算它移除了多少随机性: 简单版本:更多前导零 = 移除更多随机性 精确公式:- 有16个前导零的区块:移除 1/65,536 个状态
- 有17个前导零的区块:移除 1/131,072 个状态(稀有度翻倍!)
步骤 2:计算链总和
对于整条区块链,我们将所有单个区块熵相乘: 公式:- 区块 1:1/65,536
- 区块 2:1/65,536
- 区块 3:1/131,072
- 总计:(1/65,536) × (1/65,536) × (1/131,072) = 5630亿分之一
实际实现:使用对数
问题:这些数字很快变得巨大!仅仅10个区块后,我们就要处理大到无法有效存储的数字。 解决方案:我们使用对数将乘法转换为加法,而不是存储实际的乘法结果。 工作原理:- 传统存储:1/65,536 × 1/65,536 × 1/131,072 = 0.000000000000234
- 对数存储:16 + 16 + 17 = 49 位熵
- 可管理数字:加法而不是天文数字乘法
- 精确精度:比较中没有准确性损失
- 高效存储:Quai 使用64位存储每条链的总熵
- 简单比较:更高的熵数字 = 更安全的链
关键要点:PoEM 测量重建任何区块链的确切概率,在选择竞争链时给它完美的客观性。最难重建的链总是获胜。
