単一ブロックからチェーン全体へ
PoEMが単一ブロックで正確な作業を測定する方法を見てきました。しかし、ブロックチェーン全体をどのように比較するのでしょうか?ここで総エントロピーが登場します。 このように考えてください:- 単一ブロック:「この数学問題はどのくらい難しかったか?」
- ブロックチェーン全体:「この数学問題のシリーズ全体はどのくらい難しかったか?」
なぜ「作業」ではなくエントロピーなのか?
エントロピーは、ランダム性や無秩序を測定する物理学の概念です。マイナーがブロックを見つけるとき、本質的に非常に特定的で秩序だったハッシュを見つけることでランダム性を減少させています。 重要な洞察:除去されたランダム性の量(減少したエントロピー)は、その秩序を作るために費やされたエネルギーに直接対応します。 実世界の類推:- 散らかった部屋(高エントロピー) → きれいな部屋(低エントロピー)
- 整理に必要なエネルギー = 減少したエントロピー
- より整理された = より多くのエネルギー費やされた = より低いエントロピー
幾何学的対線形:なぜ重要か
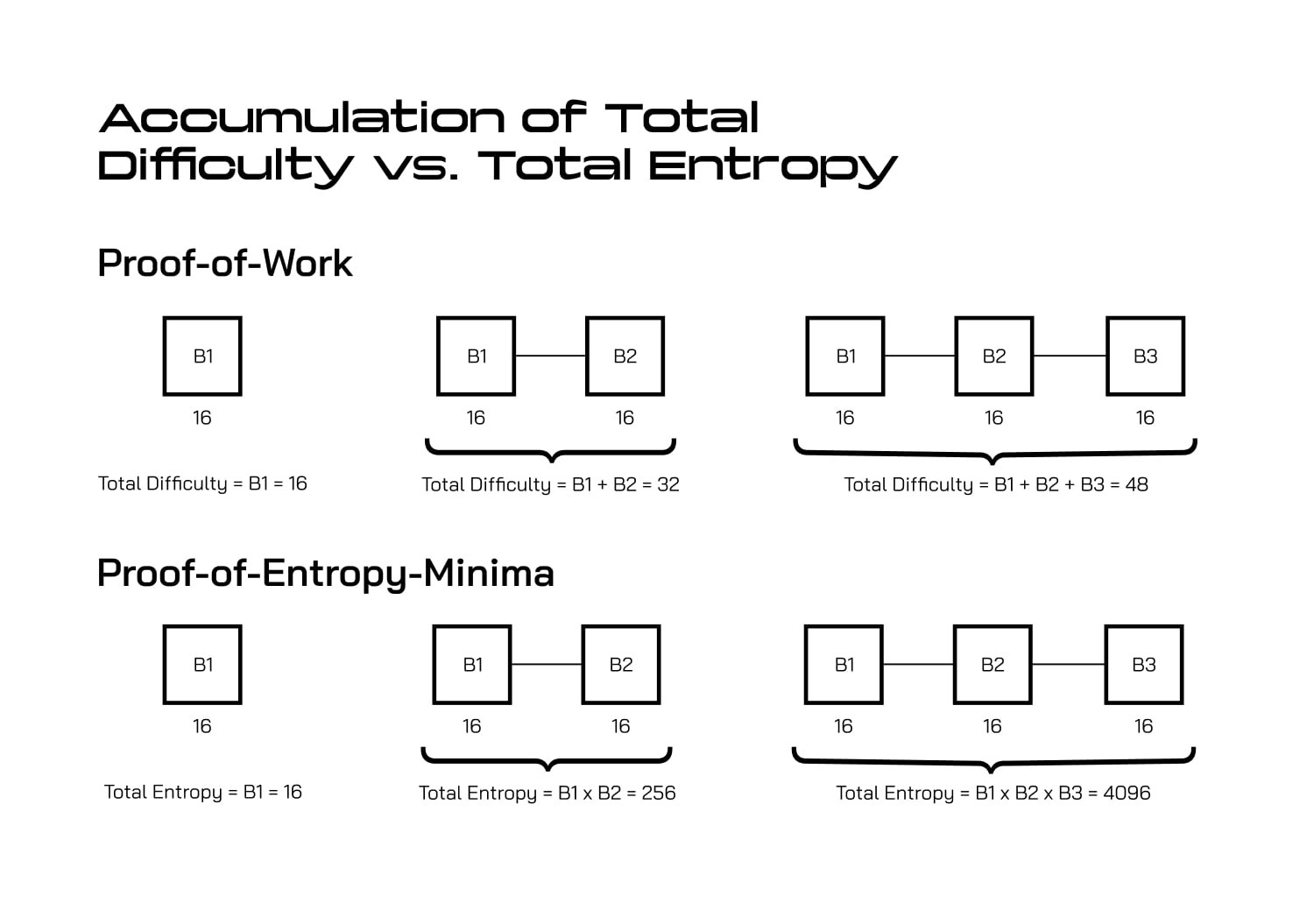
従来のPoW(線形加算):- ブロック1:16困難度ポイント
- ブロック2:16困難度ポイント
- ブロック3:16困難度ポイント
- 合計:16 + 16 + 16 = 48ポイント
- ブロック1:可能な状態の1/65536を除去
- ブロック2:残り状態の1/65536を除去
- ブロック3:残り状態の1/65536を除去
- 合計:(1/65536) × (1/65536) × (1/65536) = はるかに多くのセキュリティ
- 指数的セキュリティ:各ブロックがチェーンを指数的に再作成しにくくする
- 実際の確率:作業を再作成する実際の確率を反映
- より良い比較:どのチェーンがより多くの総エネルギーを必要としたかをより正確に測定
複利のように考えてください:10%を3回加算すると130%になりますが、10%を3回複利にすると133.1%になります。多くのブロックにわたって差は大きくなります。
ステップバイステップ計算
ステップ1:単一ブロックエントロピーの計算
各ブロックについて、それが除去したランダム性の量を計算します: 簡単バージョン:より多くの先頭ゼロ = より多くのランダム性除去 正確な公式:- 16個の先頭ゼロを持つブロック:1/65,536状態除去
- 17個の先頭ゼロを持つブロック:1/131,072状態除去(2倍稀少!)
ステップ2:チェーン合計の計算
ブロックチェーン全体について、すべての個別ブロックエントロピーを掛け合わせます: 公式:- ブロック1:1/65,536
- ブロック2:1/65,536
- ブロック3:1/131,072
- 合計:(1/65,536) × (1/65,536) × (1/131,072) = 563兆分の1
実用的実装:対数の使用
問題:これらの数値は急速に巨大になります!わずか10ブロック後、効率的に保存するには大きすぎる数値を扱うことになります。 解決策:実際の乗算結果を保存する代わりに、対数を使用して乗算を加算に変換します。 動作方法:- 従来の保存:1/65,536 × 1/65,536 × 1/131,072 = 0.000000000000234
- 対数保存:16 + 16 + 17 = 49ビットのエントロピー
- 管理可能な数値:天文学的乗算の代わりに加算
- 正確な精度:比較で精度の損失なし
- 効率的保存:Quaiはチェーンあたり総エントロピーを保存するために64ビットを使用
- 簡単比較:より高いエントロピー数値 = より安全なチェーン
重要なポイント:PoEMは任意のブロックチェーンを再作成する正確な確率を測定し、競合チェーン間で選択する際に完璧な客観性を提供します。再作成が最も困難なチェーンが常に勝ちます。
